Смещение показательной функции. Преобразование графиков функций

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

Введение

Преобразование графиков функции является одним из основных математических понятий, непосредственно связанные с практической деятельностью. Преобразование графиков функций впервые встречается в алгебре 9 класса при изучении темы «Квадратичная функция». Квадратичная функция вводится и изучается в тесной связи с квадратными уравнениями и неравенствами. Так же многие математические понятия рассматриваются графическими методами, например в 10 - 11 классах исследование функции дает возможность найти область определения и область значения функции, области убывания или возрастания, асимптоты, интервалы знакопостоянства и др. Так же этот немаловажный вопрос выносится на ГИА. Отсюда следует, построение, и преобразование графиков функции является одной из главных задач обучения математике в школе.

Однако для построения графиков многих функций можно использовать ряд методов, облегчающих построение. Выше сказанное определяет актуальность темы исследования.

Объектом исследования является изучение преобразование графиков в школьной математике.

Предмет исследования - процесс построение и преобразование графиков функции в общеобразовательной школе.

Проблемный вопрос : можно ли построить график не знакомой функции, имея навык преобразования графиков элементарных функций?

Цель: построение графиков функции в незнакомой ситуации.

Задачи:

1. Проанализировать учебный материал по исследуемой проблеме. 2. Выявить схемы преобразования графиков функции в школьном курсе математики. 3. Отобрать наиболее эффективные методы и средства построение и преобразование графиков функции. 4.Уметь применять данную теории в решении задач.

Необходимые начальные знания, умения, навыки:

Определять значение функции по значению аргумента при различных способах задания функции;

Строить графики изученных функций;

Описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;

Описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.

Основная часть

Теоретическая часть

В качестве исходного графика функции y = f(x) выберу квадратичную функциюy = x 2 . Рассмотрю случаи преобразования данного графика, связанные с изменениями формулы, задающей эту функцию и сделаю выводы для любой функции.

1. Функция y = f(x) + a

В новой формуле значения функции (ординаты точек графика) изменяются на число a, по сравнению со «старым» значением функции. Это приводит к параллельному переносу графика функции вдоль оси OY:

вверх, если a > 0; вниз, если a < 0.

ВЫВОД

Таким образом график функции y=f(x)+a, получается из графика функции y=f(x) с помощью параллельного переноса вдоль оси ординат на a единиц вверх, если a > 0, и на a единиц вниз, если a < 0.

2. Функция y = f(x-a),

В новой формуле значения аргумента (абсциссы точек графика) изменяются на число a, по сравнению со «старым» значением аргумента. Это приводит к параллельному переносу графика функции вдоль оси OX: вправо, если a < 0, влево, если a >0.

ВЫВОД

Значит график функции y= f(x - a), получается из графика функции y=f(x) с помощью параллельного переноса вдоль оси абсцисс на a единиц влево, если a > 0, и на a единиц вправо, если a < 0.

3. Функция y = k f(x), где k > 0 и k ≠ 1

В новой формуле значения функции (ординаты точек графика) изменяются в k раз, по сравнению со «старым» значением функции. Это приводит к: 1) «растяжению» от точки (0; 0) вдоль оси ОY в k раз, если k > 1, 2) «сжатию» к точке (0; 0) вдоль оси OY в раз, если 0 < k < 1.

ВЫВОД

Следовательно: чтобы построить график функции y = kf(x), где k > 0 и k ≠ 1 нужно ординаты точек заданного графика функции y = f(x) умножить на k. Такое преобразование называется растяжением от точки (0; 0) вдоль оси ОY в k раз, если k > 1; сжатием к точке (0; 0) вдоль оси OY в раз, если 0 < k < 1.

4. Функция y = f(kx), где k > 0 и k ≠ 1

В новой формуле значения аргумента (абсциссы точек графика) изменяются в k раз, по сравнению со «старым» значением аргумента. Это приводит к: 1) «растяжению» от точки (0; 0) вдоль оси ОX в 1/k раз, если 0 < k < 1; 2) «сжатию» к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

ВЫВОД

И так: чтобы построить график функции y = f(kx), где k > 0 и k ≠ 1 нужно абсциссы точек заданного графика функции y=f(x) умножить на k. Такое преобразование называется растяжением от точки (0; 0) вдоль оси ОX в 1/k раз, если 0 < k < 1, сжатием к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

5. Функция y = - f (x).

В данной формуле значения функции (ординаты точек графика) изменяются на противоположные. Это изменение приводит к симметричному отображению исходного графика функции относительно оси Ох.

ВЫВОД

Для построения графика функции y = - f (x) необходимо график функции y= f(x)

симметрично отразить относительно оси OX. Такое преобразование называется преобразованием симметрии относительно оси OX .

6. Функция y = f (-x).

В данной формуле значения аргумента (абсциссы точек графика) изменяются на противоположные. Это изменение приводит к симметричному отображению исходного графика функции относительно оси ОY.

Пример для функции у = - х² это преобразование не заметно, т. к. данная функция чётная и график после преобразования не меняется. Это преобразование видно, когда функция нечётная и когда ни чётная и ни нечётная.

7. Функция y = |f(x)|.

В новой формуле значения функции (ординаты точек графика) находятся под знаком модуля. Это приводит к исчезновению частей графика исходной функции с отрицательными ординатами (т.е. находящихся в нижней полуплоскости относительно оси Ох) и симметричному отображению этих частей относительно оси Ох.

8. Функция y= f (|x|).

В новой формуле значения аргумента (абсциссы точек графика) находятся под знаком модуля. Это приводит к исчезновению частей графика исходной функции с отрицательными абсциссами (т.е. находящихся в левой полуплоскости относительно оси ОY) и замещению их частями исходного графика, симметричными относительно оси ОY.

Практическая часть

Рассмотрим несколько примеров применения вышеизложенной теории.

ПРИМЕР 1.

Решение. Преобразуем данную формулу:

1) Построим график функции

ПРИМЕР 2.

Построить график функции, заданной формулой

Решение. Преобразуем данную формулу, выделив в данном квадратном трехчлене квадрат двучлена:

1) Построим график функции

2) Выполним параллельный перенос построенного графика на вектор

ПРИМЕР 3.

ЗАДАНИЕ ИЗ ЕГЭПостроение графика кусочной функции

График функции График функции y=|2(x-3)2-2|; 1

Основные элементарные функции в чистом виде без преобразования встречаются редко, поэтому чаще всего приходится работать с элементарными функциями, которые получили из основных с помощью добавления констант и коэффициентов. Такие графики строятся при помощи геометрических преобразований заданных элементарных функций.

Рассмотрим на примере квадратичной функции вида y = - 1 3 x + 2 3 2 + 2 , графиком которой является парабола y = x 2 , которая сжата втрое относительно О у и симметрична относительно О х, причем сдвинутую на 2 3 по О х вправо, на 2 единицы по О у вверх. На координатной прямой это выглядит так:

Yandex.RTB R-A-339285-1

Геометрические преобразования графика функции

Применяя геометрические преобразования заданного графика получаем, что график изображается функцией вида ± k 1 · f (± k 2 · (x + a)) + b , когда k 1 > 0 , k 2 > 0 являются коэффициентами сжатия при 0 < k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 > 1 , k 2 > 1 вдоль О у и О х. Знак перед коэффициентами k 1 и k 2 говорит о симметричном отображении графика относительно осей, a и b сдвигают ее по О х и по О у.

Определение 1

Существует 3 вида геометрических преобразований графика :

• Масштабирование вдоль О х и О у. На это влияют коэффициенты k 1 и k 2 при условии не равности 1 , когда 0 < k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 > 1 , k 2 > 1 , то график растягивается по О у и сжимается по О х.
• Симметричное отображение относительно координатных осей. При наличии знака « - » перед k 1 симметрия идет относительно О х, перед k 2 идет относительно О у. Если « - » отсутствует, тогда пункт при решении пропускается;
• Параллельный перенос (сдвиг) вдоль О х и О у. Преобразование производится при наличии коэффициентов a и b неравных 0 . Если значение a положительное, до график сдвигается влево на | а | единиц, если отрицательное a , тогда в право на такое же расстояние. Значение b определяет движение по оси О у, что значит при положительном b функция движется вверх, при отрицательном – вниз.

Рассмотрим решения на примерах, начиная со степенной функции.

Пример 1

Преобразовать y = x 2 3 и построить график функции y = - 1 2 · 8 x - 4 2 3 + 3 .

Решение

Представим функции таким образом:

y = - 1 2 · 8 x - 4 2 3 + 3 = - 1 2 · 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3

Где k 1 = 2 , стоит обратить внимание на наличие « - » , а = - 1 2 , b = 3 . Отсюда получаем, что геометрические преобразования производятся с растяжения вдоль О у вдвое, отображается симметрично относительно О х, сдвигается вправо на 1 2 и вверх на 3 единицы.

Если изобразить исходную степенную функцию, получим, что

при растягивании вдвое вдоль О у имеем, что

Отображение, симметричное относительно О х, имеет вид

а движение вправо на 1 2

движение на 3 единицы вверх имеет вид

Преобразования показательной функции рассмотрим на примерах.

Пример 2

Произвести построение графика показательной функции y = - 1 2 1 2 (2 - x) + 8 .

Решение.

Преобразуем функцию, исходя из свойств степенной функции. Тогда получим, что

y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 · 1 2 - 1 2 x + 8

Отсюда видно, что получим цепочку преобразований y = 1 2 x:

y = 1 2 x → y = 1 2 · 1 2 x → y = 1 2 · 1 2 1 2 x → → y = - 1 2 · 1 2 1 2 x → y = - 1 2 · 1 2 - 1 2 x → → y = - 1 2 · 1 2 - 1 2 x + 8

Получаем, что исходная показательная функция имеет вид

Сжимание вдвое вдоль О у дает

Растягивание вдоль О х

Симметричное отображение относительно О х

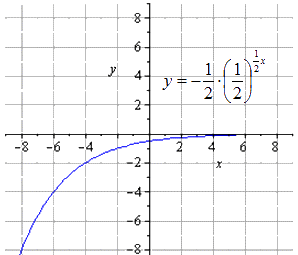
Отображение симметрично относительно О у

Сдвигание на 8 единиц вверх

Рассмотрим решение на примере логарифмической функции y = ln (x) .

Пример 3

Построить функцию y = ln e 2 · - 1 2 x 3 при помощи преобразования y = ln (x) .

Решение

Для решения необходимо использовать свойства логарифма, тогда получаем:

y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2

Преобразования логарифмической функции выглядят так:

y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2

Изобразим график исходной логарифмической функции

Производим сжимание строе по О у

Производим растягивание вдоль О х

Производим отображение относительно О у

Производим сдвигание вверх на 2 единицы, получаем

Для преобразования графиков тригонометрической функциинеобходимо подгонять под схему решения вида ± k 1 · f (± k 2 · (x + a)) + b . Необходимо, чтобы k 2 приравнивался к T k 2 . Отсюда получаем, что 0 < k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

Рассмотрим примеры решения заданий с преобразованиями y = sin x .

Пример 4

Построить график y = - 3 sin 1 2 x - 3 2 - 2 с помощью преобразований функции y=sinx.

Решение

Необходимо привести функцию к виду ± k 1 · f ± k 2 · x + a + b . Для этого:

y = - 3 sin 1 2 x - 3 2 - 2 = - 3 sin 1 2 (x - 3) - 2

Видно, что k 1 = 3 , k 2 = 1 2 , a = - 3 , b = - 2 . Так как перед k 1 имеется « - » , а перед k 2 - нет, тогда получим цепочку преобразований вида:

y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = - 3 sin 1 2 x → → y = - 3 sin 1 2 x - 3 → y = - 3 sin 1 2 (x - 3) - 2

Подробное преобразование синусоиды. При построении графика исходной синусоиды y = sin (x) получаем, что наименьшим положительным периодом считается T = 2 π . Нахождение максимума в точках π 2 + 2 π · k ; 1 , а минимума - - π 2 + 2 π · k ; - 1 , k ∈ Z .

Производится растягивание по О у втрое, значит возрастание амплитуды колебаний возрастет в 3 раза. T = 2 π - это наименьший положительный период. Максимумы переходят в π 2 + 2 π · k ; 3 , k ∈ Z , минимумы - - π 2 + 2 π · k ; - 3 , k ∈ Z .

При растягивании по О х вдвое получаем, что наименьший положительный период увеличивается в 2 раза и равняется T = 2 π k 2 = 4 π . Максимумы переходят в π + 4 π · k ; 3 , k ∈ Z , минимумы – в - π + 4 π · k ; - 3 , k ∈ Z .

Изображение производится симметрично относительно О х. Наименьший положительный период в данном случае не меняется и равняется T = 2 π k 2 = 4 π . Переход максимума выглядит как - π + 4 π · k ; 3 , k ∈ Z , а минимума – π + 4 π · k ; - 3 , k ∈ Z .

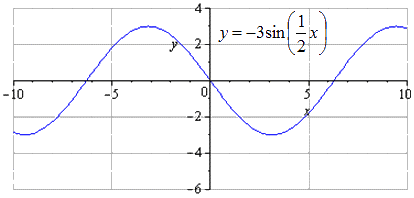
Производится сдвижение графика вниз на 2 единицы. Изменение наименьшего общего периода не происходит. Нахождение максимумов с перехождением в точки - π + 3 + 4 π · k ; 1 , k ∈ Z , минимумов - π + 3 + 4 π · k ; - 5 , k ∈ Z .

На данном этапе график тригонометрической функции считается преобразованным.

Рассмотрим подробное преобразование функции y = cos x .

Пример 5

Построить график функции y = 3 2 cos 2 - 2 x + 1 при помощи преобразования функции вида y = cos x .

Решение

По алгоритму необходимо заданную функцию привести к виду ± k 1 · f ± k 2 · x + a + b . Тогда получаем, что

y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1

Из условия видно, что k 1 = 3 2 , k 2 = 2 , a = - 1 , b = 1 , где k 2 имеет « - » , а перед k 1 он отсутствует.

Отсюда получаем, что получится график тригонометрической функции вида:

y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1)) → y = 3 2 cos - 2 (x - 1) + 1

Пошаговое преобразование косинусоиды с графической иллюстрацией.

При заданной графике y = cos (x) видно, что наименьший общий период равняется T = 2 π . Нахождение максимумов в 2 π · k ; 1 , k ∈ Z , а минимумов π + 2 π · k ; - 1 , k ∈ Z .

При растягивании вдоль О у в 3 2 раза происходит возрастание амплитуды колебаний в 3 2 раза. T = 2 π является наименьшим положительным периодом. Нахождение максимумов в 2 π · k ; 3 2 , k ∈ Z , минимумов в π + 2 π · k ; - 3 2 , k ∈ Z .

При сжатии вдоль О х вдвое получаем, что наименьшим положительным периодом является число T = 2 π k 2 = π . Производится переход максимумов в π · k ; 3 2 , k ∈ Z ,минимумов - π 2 + π · k ; - 3 2 , k ∈ Z .

Симметричное отображение относительно О у. Так как график нечетный, то он не будет изменяться.

При сдвигании графика на 1 . Отсутствуют изменения наименьшего положительного периода T = π . Нахождение максимумов в π · k + 1 ; 3 2 , k ∈ Z , минимумов - π 2 + 1 + π · k ; - 3 2 , k ∈ Z .

При сдвигании на 1 наименьший положительный период равняется T = π и не изменен. Нахождение максимумов в π · k + 1 ; 5 2 , k ∈ Z , минимумов в π 2 + 1 + π · k ; - 1 2 , k ∈ Z .

Преобразования функции косинуса завершено.

Рассмотрим преобразования на примере y = t g x .

Пример 6

Построить график функции y = - 1 2 t g π 3 - 2 3 x + π 3 при помощи преобразований функции y = t g (x) .

Решение

Для начала необходимо привести заданную функцию к виду ± k 1 · f ± k 2 · x + a + b , после чего получаем, что

y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3

Отчетливо видно, что k 1 = 1 2 , k 2 = 2 3 , a = - π 2 , b = π 3 , а перед коэффициентами k 1 и k 2 имеется « - » . Значит, после преобразования тангенсоиды получаем

y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3

Поэтапное преобразование тангенсоиды с графическим изображением.

Имеем, что исходный график – это y = t g (x) . Изменение положительного периода равняется T = π . Областью определения считается - π 2 + π · k ; π 2 + π · k , k ∈ Z .

Сжимаем в 2 раза вдоль О у. T = π считается наименьшим положительным периодом, где область определения имеет вид - π 2 + π · k ; π 2 + π · k , k ∈ Z .

Растягиваем вдоль О х в 3 2 раза. Вычислим наименьший положительный период, причем равнялся T = π k 2 = 3 2 π . А область определения функции с координатами - 3 π 4 + 3 2 π · k ; 3 π 4 + 3 2 π · k , k ∈ Z , меняется только область определения.

Симметрия идет по сторону О х. Период не изменится в этот момент.

Необходимо симметрично отображать оси координат. Область определения в данном случае неизменна. График совпадает с предыдущим. Это говорит о том, что функция тангенса нечетная. Если к нечетной функции задать симметричное отображение О х и О у, тогда преобразуем до исходной функции.

Параллельный перенос.

ПЕРЕНОС ВДОЛЬ ОСИ ОРДИНАТ

f(x) => f(x) - b
Пусть требуется построить график функции у = f(х) - b. Нетрудно заметить, что ординаты этого графика для всех значений x на |b| единиц меньше соответствующих ординат графика функций у = f(х) при b>0 и на |b| единиц больше - при b 0 или вверх при b Для построения графика функции y + b = f(x) следует построить график функции y = f(x) и перенести ось абсцисс на |b| единиц вверх при b>0 или на |b| единиц вниз при b

ПЕРЕНОС ВДОЛЬ ОСИ АБСЦИСС

f(x) => f(x + a)
Пусть требуется построить график функции у = f(x + a). Рассмотрим функцию y = f(x), которая в некоторой точке x = x1 принимает значение у1 = f(x1). Очевидно, функция у = f(x + a) примет такое же значение в точке x2, координата которой определяется из равенства x2 + a = x1, т.е. x2 = x1 - a, причем рассматриваемое равенство справедливо для совокупности всех значений из области определения функции. Следовательно, график функции у = f(x + a) может быть получен параллельным перемещением графика функции y = f(x) вдоль оси абсцисс влево на |a| единиц при a > 0 или вправо на |a| единиц при a Для построения графика функции y = f(x + a) следует построить график функции y = f(x) и перенести ось ординат на |a| единиц вправо при a>0 или на |a| единиц влево при a

Примеры:

1.y=f(x+a)

2.y=f(x)+b

Отражение.

ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ВИДА Y = F(-X)

f(x) => f(-x)
Очевидно, что функции y = f(-x) и y = f(x) принимают равные значения в точках, абсциссы которых равны по абсолютной величине, но противоположны по знаку. Иначе говоря, ординаты графика функции y = f(-x) в области положительных (отрицательных) значений х будут равны ординатам графика функции y = f(x) при соответствующих по абсолютной величине отрицательных (положительных) значениях х. Таким образом, получаем следующее правило.
Для построения графика функции y = f(-x) следует построить график функции y = f(x) и отразить его относительно оси ординат. Полученный график является графиком функции y = f(-x)

ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ВИДА Y = - F(X)

f(x) => - f(x)
Ординаты графика функции y = - f(x) при всех значениях аргумента равны по абсолютной величине, но противоположны по знаку ординатам графика функции y = f(x) при тех же значениях аргумента. Таким образом, получаем следующее правило.
Для построения графика функции y = - f(x) следует построить график функции y = f(x) и отразить его относительно оси абсцисс.

Примеры:

1.y=-f(x)

2.y=f(-x)

3.y=-f(-x)

Деформация.

ДЕФОРМАЦИЯ ГРАФИКА ВДОЛЬ ОСИ ОРДИНАТ

f(x) => k f(x)
Рассмотрим функцию вида y = k f(x), где k > 0. Нетрудно заметить, что при равных значениях аргумента ординаты графика этой функции будут в k раз больше ординат графика функции у = f(x) при k > 1 или 1/k раз меньше ординат графика функции y = f(x) при k Для построения графика функции y = k f(x) следует построить график функции y = f(x) и увеличить его ординаты в k раз при k > 1(произвести растяжение графика вдоль оси ординат) или уменьшить его ординаты в 1/k раз при k
k > 1 - растяжение от оси Ох
0 - сжатие к оси OX

ДЕФОРМАЦИЯ ГРАФИКА ВДОЛЬ ОСИ АБСЦИСС

f(x) => f(k x)
Пусть требуется построить график функции y = f(kx), где k>0. Рассмотрим функцию y = f(x), которая в произвольной точке x = x1 принимает значение y1 = f(x1). Очевидно, что функция y = f(kx) принимает такое же значение в точке x = x2, координата которой определяется равенством x1 = kx2, причем это равенство справедливо для совокупности всех значений х из области определения функции. Следовательно, график функции y = f(kx) оказывается сжатым (при k 1) вдоль оси абсцисс относительно графика функции y = f(x). Таким образом, получаем правило.
Для построения графика функции y = f(kx) следует построить график функции y = f(x) и уменьшить его абсциссы в k раз при k>1 (произвести сжатие графика вдоль оси абсцисс) или увеличить его абсциссы в 1/k раз при k
k > 1 - сжатие к оси Оу
0 - растяжение от оси OY

Работу выполнили Чичканов Александр, Леонов Дмитрий под руководством Ткач Т.В, Вязовова С.М, Островерховой И.В.
©2014